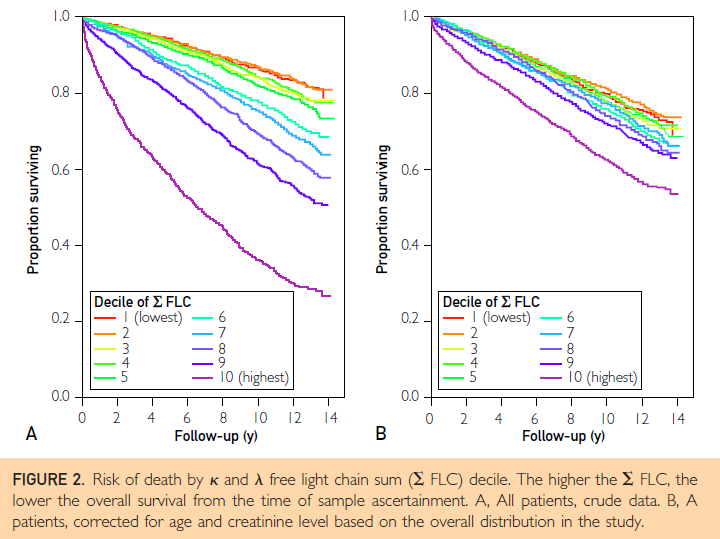
survivalパッケージのサンプルデータセットflchain (free light chain)は、The Olmsted County MGUS prevalence cohortに登録された米国の一般住民において血清遊離軽鎖レベルと全死亡の関連を報告した下記の論文で使用されたデータセットの一部です。
Research Question
下記のresearch quetionをテーマにした研究論文を、EZRを利用してflchainデータセットから作成してみましょう。
- 研究デザイン:コホート研究
- 対象:The Olmsted County MGUS prevalence cohortの登録者の一部
- 暴露因子&比較因子:free light chainの四分位 (flc4)
- アウトカム:全死亡
- 共変量(補正因子):年齢、性別、MGUS
- 統計解析:多変量補正Cox比例ハザードモデル
flchainデータセットのEZRへの読み込みとflc4変数の作成方法については下記ページを参照して下さい。
Kaplan-Meier曲線を作成する
Kaplan-Meier法を利用して、遊離軽鎖4分位別の累積死亡率を算出します。
EZRメニューの統計解析 > 生存期間の解析 > 生存曲線の記述と群間の比較(Log-rank検定) を選択します。
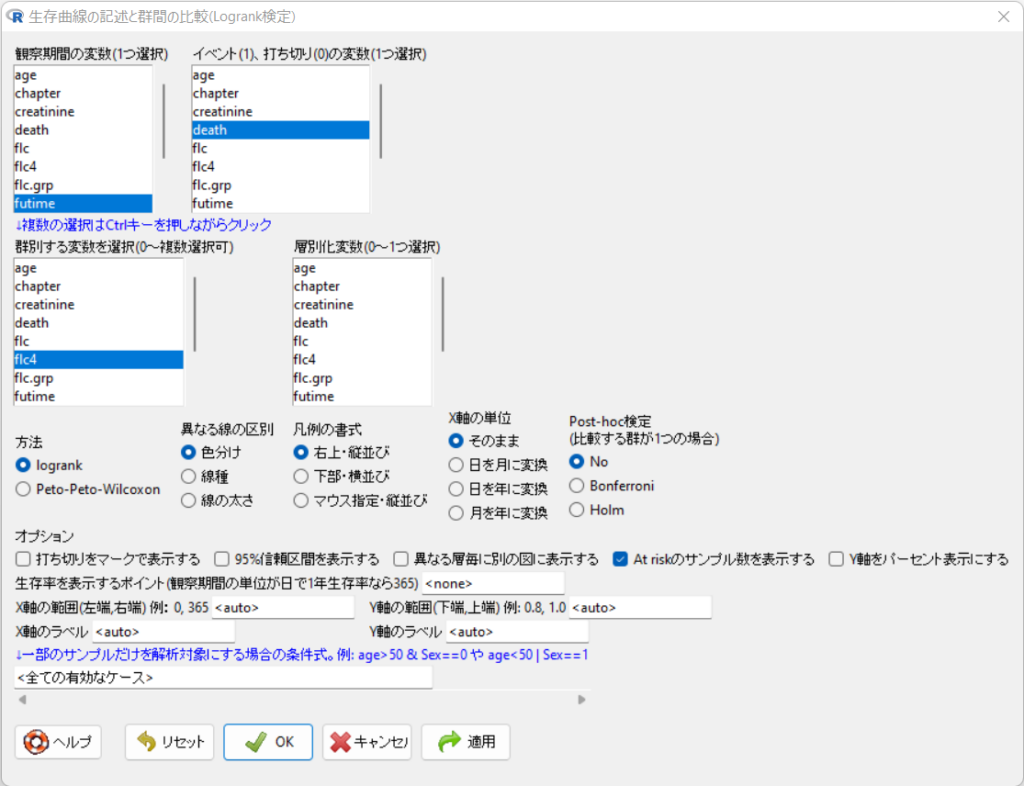
- 「観察期間の変数(1つ選択)」から”futime”を選択します。
- 「イベント(1)、打ち切り(0)の変数(1つ選択)」から”death”を選択します。
- 「群別する変数を選択(0~複数選択可)」から”flc4″を選択します。
- 「オプション」の「打ち切りをマークで表示する」のチェックを外します。
- OKボタンをクリックします。
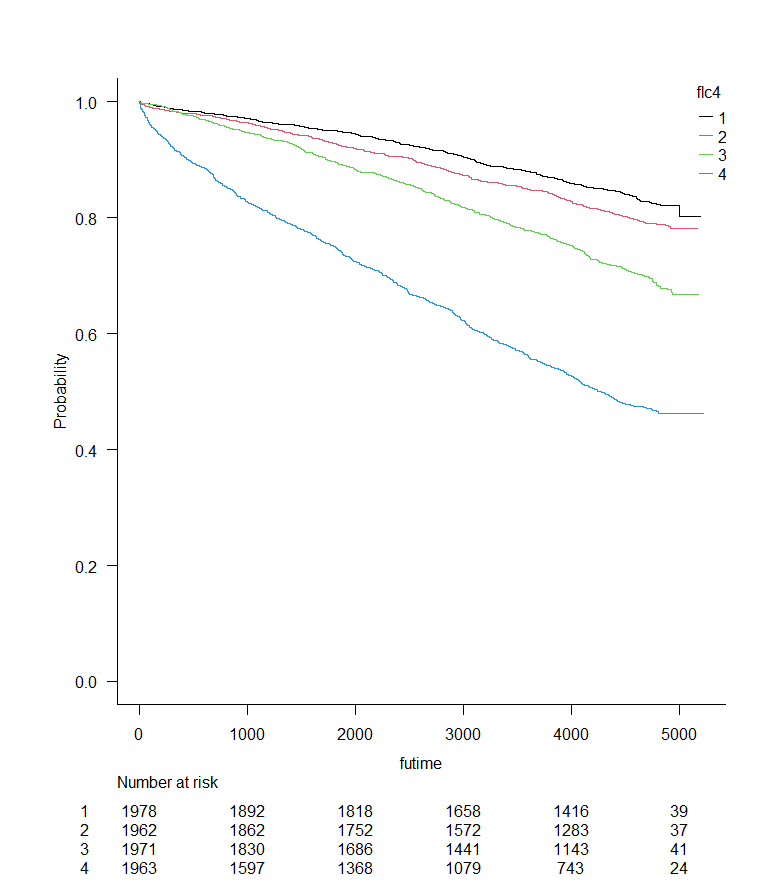
遊離軽鎖4分位別の生存曲線が作成され、Log-rank検定の結果が出力されます。
Call:
survdiff(formula = Surv(futime, death == 1) ~ flc4, data = flchain,
na.action = na.omit, rho = 0)
N Observed Expected (O-E)^2/E (O-E)^2/V
flc4=1 1978 311 606 143.877 200.1093
flc4=2 1962 369 577 75.087 102.3676
flc4=3 1971 543 547 0.031 0.0414
flc4=4 1963 946 438 587.961 740.2260
Chisq= 811 on 3 degrees of freedom, p= <2e-16
P < 0.05ですので、遊離軽鎖4分位別の累積生存率には統計学的に有意な差を認めます。
サブグループ解析
第1分位と第2分位の累積生存率を比較する場合、サブグループを指定する条件式を追加します。
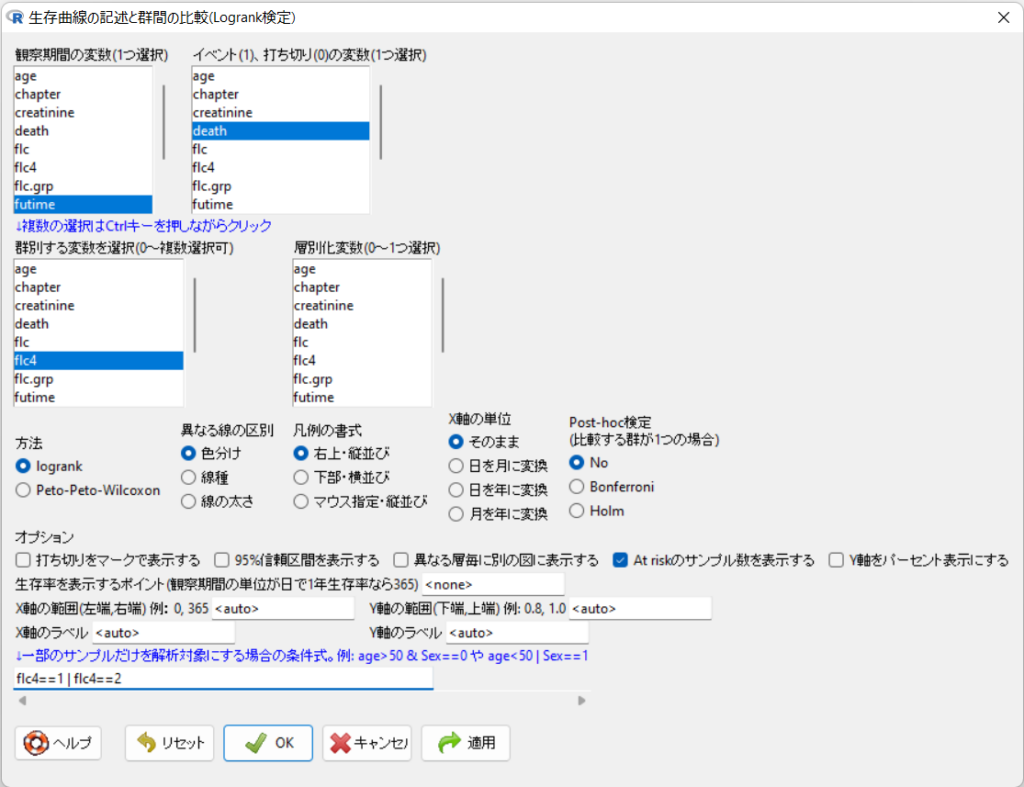
- 「観察期間の変数(1つ選択)」から”futime”を選択します。
- 「イベント(1)、打ち切り(0)の変数(1つ選択)」から”death”を選択します。
- 「群別する変数を選択(0~複数選択可)」から”flc4″を選択します。
- 「オプション」の「打ち切りをマークで表示する」のチェックを外します。
- 「↓一部のサンプルだけを解析対象にする場合の条件式」に”flc4==1 | flc4==2″を入力します。
- OKボタンをクリックします。
Call:
survdiff(formula = Surv(futime, death == 1) ~ flc4, data = flchain,
subset = flc4 == 1 | flc4 == 2, na.action = na.omit, rho = 0)
N Observed Expected (O-E)^2/E (O-E)^2/V
flc4=1 1978 311 349 4.15 8.53
flc4=2 1962 369 331 4.38 8.53
Chisq= 8.5 on 1 degrees of freedom, p= 0.003P = 0.003ですので、第1分位群と第2分位群の累積生存率の差は統計学的に有意です。