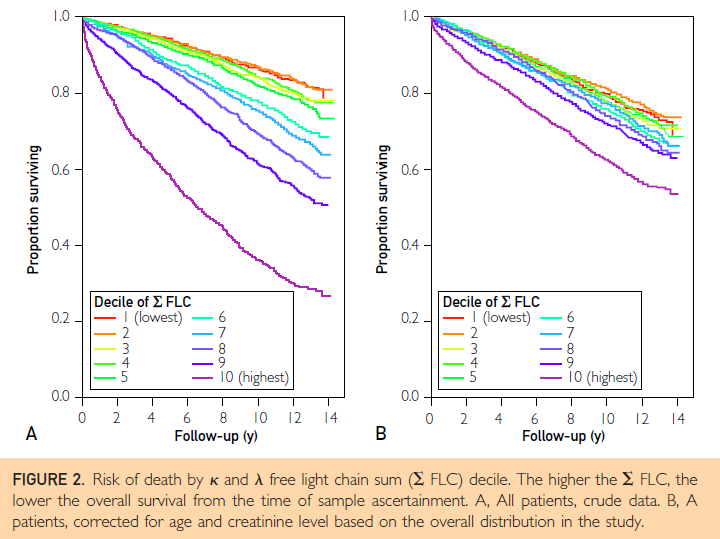
survivalパッケージのサンプルデータセットflchain (free light chain)は、The Olmsted County MGUS prevalence cohortに登録された米国の一般住民において血清遊離軽鎖レベルと全死亡の関連を報告した下記の論文で使用されたデータセットの一部です。
Research Question
下記のresearch quetionをテーマにした研究論文を、EZRを利用してflchainデータセットから作成してみましょう。
- 研究デザイン:コホート研究
- 対象:The Olmsted County MGUS prevalence cohortの登録者の一部
- 暴露因子&比較因子:free light chainの四分位 (flc4)
- アウトカム:全死亡
- 共変量(補正因子):年齢、性別、MGUS
- 統計解析:多変量補正Cox比例ハザードモデル
flchainデータセットのEZRへの読み込みとflc4変数の作成方法については下記ページを参照して下さい。
ベースライン所見の表を作成する
遊離軽鎖4分位別の年齢、性別、MGUSの分布を示す表を作成します。
| 遊離軽鎖, mg/dL | 0.090-2.210 | 2.212-2.790 | 2.791-3.560 | 3.560-43.00 | P値 |
| 人数 | 1978 | 1962 | 1971 | 1963 | |
| 年齢, 歳 | 59 (50, 67) | 61 (54, 69) | 63 (56, 71) | 70 (60, 78) | <0.05 |
| 性別, 人(%) | 772 (39.0) | 841 (42.9) | 940 (47.7) | 971 (49.5) | <0.05 |
| MGUS, 人(%) | 104 (5.3) | 9 (0.5) | 2 (0.1) | 0 (0.0) | <0.05 |
遊離軽鎖4分位の分布を確認する
EZRメニューの統計解析 > 連続変数の解析 > 連続変数の要約 を選択します。
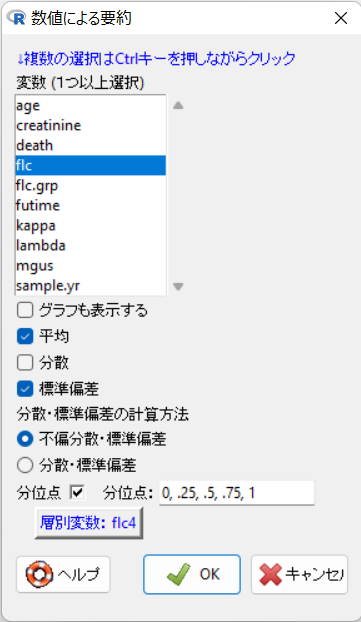
- 「変数(1つ以上選択)」から”flc”を選択します。
- 「層別して要約…」ボタンをクリックして、”flc4″を選択しします。OKボタンをクリックすると、「層別して要約…」ボタンの表示が「層別変数: flc4」に変更されます。
- OKボタンをクリックします。
mean u.sd 0% 25% 50% 75% 100% data:n
1 1.745655 0.3993577 0.090 1.52 1.8675 2.053 2.21 1978
2 2.497309 0.1668980 2.212 2.35 2.4905 2.640 2.79 1962
3 3.133323 0.2137054 2.791 2.95 3.1200 3.310 3.56 1971
4 5.168015 2.6167789 3.560 3.93 4.4300 5.350 43.00 19630%値と100%値からflc4分位の範囲を確認できます。
ここで困った事態が発生していることがわかります。第3分位の最大値と第4分位の最小値が3.56と3.560なので、第3分位と第4分位の境界値がよくわかりません。flchainデータセットをflcでソートして、第3分位と第4分位の境界値を確認してみましょう。
EZRメニューのアクティブデータセット > 行の操作 > データセットの行を並び替える を選択します。flcを選択してOKボタンをクリックします。
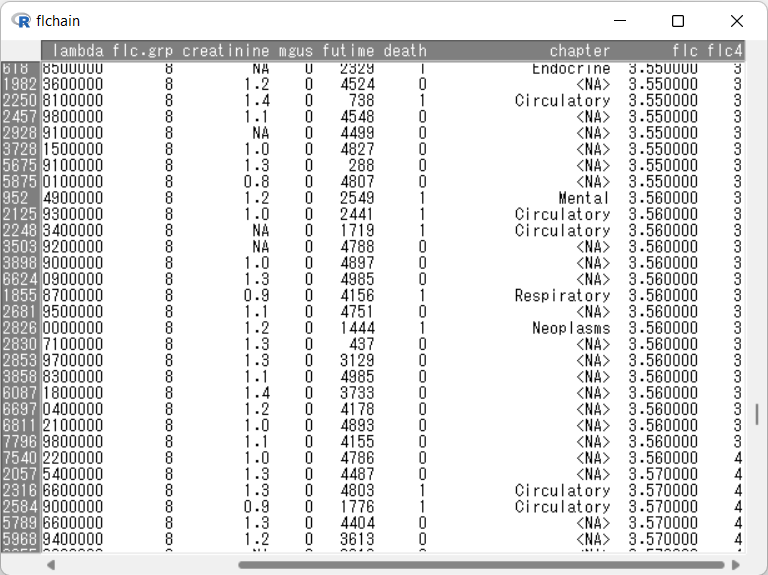
flc 3.560000の対象者のうち、一人だけ第4分位に分類されているという困った事態が発生してしまっています・・・。本来ならばflc4の値を修正しないといけませんが、とりあえずこのまま先に進むことにします。修正するならば、EZRメニューのアクティブデータセット > 変数の操作 > 計算式を入力して新たな変数を作成する をうまく使って下さい。
年齢分布を比較する
まずはヒストグラムを作成して、年齢の分布を確認します。
EZRメニューのグラフと表 > ヒストグラム を選択します。
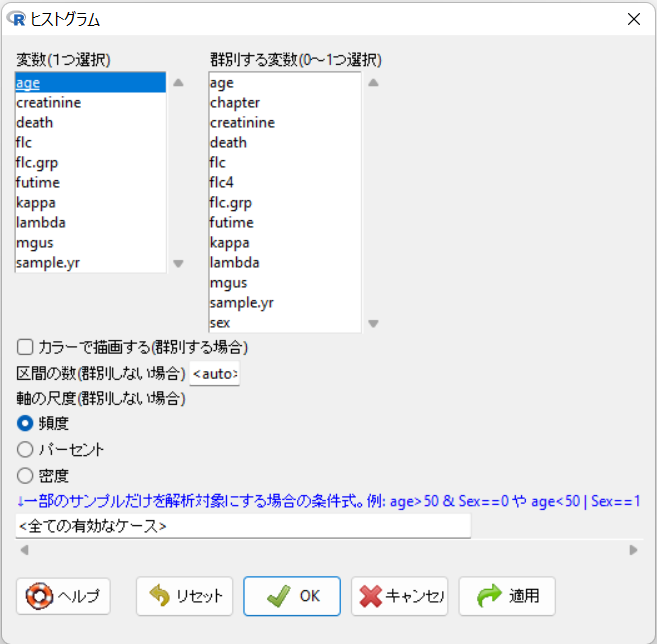
「変数(1つ選択)」から”age”を選択して、OKボタンをクリックします。
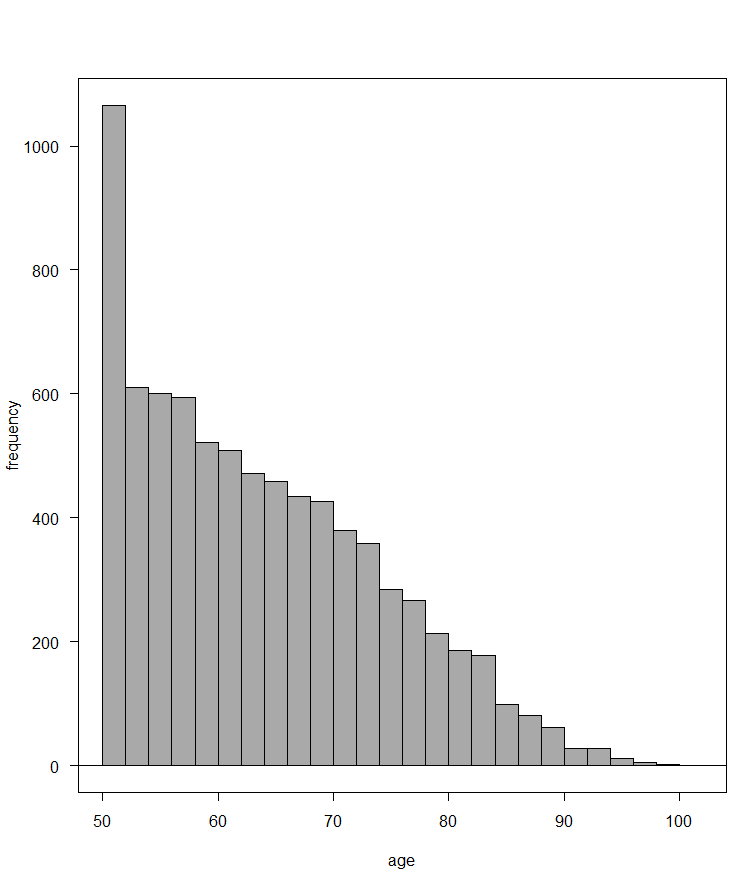
若年者ほど多く、高齢者ほど少ないので、年齢分布は中央値(0%, 75%)で表現するのが良さそうです。
EZRメニューの統計解析 > 連続変数の解析 > 連続変数の要約を選択します。
- 「変数(1つ以上選択)」から”age”を選択します。
- 「層別して要約…」 ボタンをクリックして、”flc4″を選択する。OKボタンをクリックすると、「層別して要約…」 ボタンの表示が「層別変数: fl4」に変更されます。
- OKボタンをクリックします。
mean u.sd 0% 25% 50% 75% 100% data:n
1 61.01618 8.884679 50 54 59 67 94 1978
2 62.12895 9.230196 50 54 61 69 92 1962
3 64.46778 10.141954 50 56 63 71 101 1971
4 69.58278 11.303146 50 60 70 78 100 1963これで遊離軽鎖4分位別の年齢の分布を確認できますね。
次は、年齢の群間比較を行います。「遊離軽鎖4分位の各群の年齢分布は統計学的に有意に異なっていると言えるのか?」を検定を用いて確認します。利用する検定は変数の分布によって異なります。
- 2群間の比較
- 正規分布ならば、対応のないt検定
- 非正規分布ならば、Mann-Whitney U検定 (Wilcoxon順位和検定)
- ≧3群間の比較
- 正規分布ならば、one-way ANOVA (analysis of variance)
- 非正規分布ならば、Kruskul-Wallis検定
今回は、非正規分布の年齢の4群間の比較ですから、Kruskul-Wallis検定を利用しましょう。
EZRメニューの統計解析 > ノンパラメトリック検定 > 3群以上の間の比較(Kruskul-Wallis test) を選択します。
- 「目的変数(1つ選択)」から”age”を選択します。
- 「グループ(1つ選択)」から”flc4″を選択します。
- OKボタンをクリックします。
Kruskal-Wallis rank sum test
data: age by factor(flc4)
Kruskal-Wallis chi-squared = 696.23, df = 3, p-value < 2.2e-16
P-value < 0.05なので、年齢は遊離軽鎖4分位群間で統計学的に有意に異なっていると言えます。
正規分布の変数ならば、EZRメニューの統計解析 >連続変数の解析 > 3郡以上の間の平均値の比較(一元配置分散分析One-way ANOVA) を選択して下さい。
性別分布を比較する
名義変数と名義変数の関連を評価するにはχ2検定が一般的です。χ2検定を使って、遊離軽鎖4分位群間で性別の分布が統計学的に有意に異なるかを評価しましょう。
EZRメニューの統計解析 >名義変数の解析 > 分割表の作成と群間の比率の比較 (Fisherの性格検定) を選択します。
- 「行の選択(1つ以上選択)」から”sex”を選択します。
- 「列の変数(1つ選択)」から”flc4″を選択します。
- 「仮説検定」の「カイ2乗検定」をチェックします。
- OKボタンをクリックします。
> .Table
flc4
sex 1 2 3 4
F 1206 1121 1031 992
M 772 841 940 971
> colPercents(.Table) # Column Percentages
flc4
sex 1 2 3 4
F 61 57.1 52.3 50.5
M 39 42.9 47.7 49.5
Total 100 100.0 100.0 100.0
Count 1978 1962.0 1971.0 1963.0
> .Test <- chisq.test(.Table, correct=TRUE)
> .Test
Pearson's Chi-squared test
data: .Table
X-squared = 53.551, df = 3, p-value = 1.399e-11
遊離軽鎖4分位別の性別の集計結果が示されました。χ2検定のP値 < 0.05であり、遊離軽鎖4分位間に統計学的に有意な性差があることが示されました。
MGUS分布を比較する
性別と同様に、MGUSの分布が遊離軽鎖4分位間で統計学的に有意に異なるかを評価してみましょう。
> .Table
flc4
mgus 1 2 3 4
0 1874 1953 1969 1963
1 104 9 2 0
> colPercents(.Table) # Column Percentages
flc4
mgus 1 2 3 4
0 94.7 99.5 99.9 100
1 5.3 0.5 0.1 0
Total 100.0 100.0 100.0 100
Count 1978.0 1962.0 1971.0 1963性別と大きく異なり、MGUSは極めて稀な存在です。10人未満の少数セルが存在しています。こういう場合、χ2検定よりもFisher正確検定が適切です。
> .Test <- chisq.test(.Table, correct=TRUE)
> .Test
Pearson's Chi-squared test
data: .Table
X-squared = 266.26, df = 3, p-value < 2.2e-16
> remove(.Test)
> fisher.test(.Table)
Fisher's Exact Test for Count Data
data: .Table
p-value < 2.2e-16
alternative hypothesis: two.sided
χ2検定もFisher正確検定もいずれもP-value < 0.05でした。
これで患者背景を示す表1が完成です。