Stata: discrete time hazard model
追跡期間が、連続変数ではなく、カテゴリ変数(1-2ヶ月、3-6ヶ月、7-12ヶ月等)である場合、通常のCox比例ハザードモデルではなく、discrete time hazard modelを用いた方がよい場合があります。
Discrete time hazard modelの概念については、下記の論文がよくまとまっています。
link関数をlogitにする場合とcomplementary log-logにする場合がありますが、Cox比例ハザードモデルに近いcomplementary log-log関数を利用した方がよさそうです。
2010年JAMAにdiscrete time hazard model with a complementary log-log linkを利用した論文が実際に発表されていました。
Stataのcloglogコマンドを使って、実際にdiscrete time hazard model with complementary log-log linkを行ってみましょう。
参考文献:Rabe-Hesketh S and Skrondal A. Multilevel and longitudinal model using Stata, second edition, Stata Corp LP
サンプルデータをダウンロードする
サンプルデータmortality.dtaをダウンロードします。1974-76年にガテマラで行われた15-49歳の女性とその子供を対象にした後ろ向き研究であり、母親の年齢や子供の出生順番が、子供の生存率に及ぼす影響を評価しています。1行が子供一人分のデータです。
. use http://www.stata-press.com/data/mlmus3/mortality,clear
(Child mortality in Guatemala)- kidid = 子供ID
- momid = 母親ID
- time = 子供の生存期間(月、最大60ヶ月)
- death = 子供の死亡(1 = 死亡、0 = 打ち切り)
- mage = 母親の出産時年齢
- border = 子供の出生順番
- p0014, p1523, p2435, p36up = 前の子供が生まれてからの期間(0-14ヶ月、15-23ヶ月、24-35ヶ月、36ヶ月以上)のダミー変数(兄の出生後16ヶ月で妹が生まれれば、p0014 = 0、p1523 = 1、p2435 = 0、p36up = 0)
- pdead = 前の子供の死産
- f0011とf1223 = 次の子供が生まれるまでの期間(0-11ヶ月、12-23ヶ月)のダミー変数
Discrete time hazard model用のデータシートを作成する
listコマンドを使って、momid==1のデータを確認してみます。
. list kidid momid time death mage border f0011 f1223 if momid==1, clean
kidid momid time death mage border f0011 f1223
1. 101 1 60 0 27 4 0 0
2. 102 1 60 0 30 5 0 0
3. 103 1 60 0 33 6 0 1
4. 104 1 60 0 35 7 0 0 子供生存期間timeの分布を確認してみましょう。最大値60が最も多く、不規則な分布です。
. histogram time, xsize(3.7) ysize(3.7)
(bin=41, start=.25, width=1.4573171)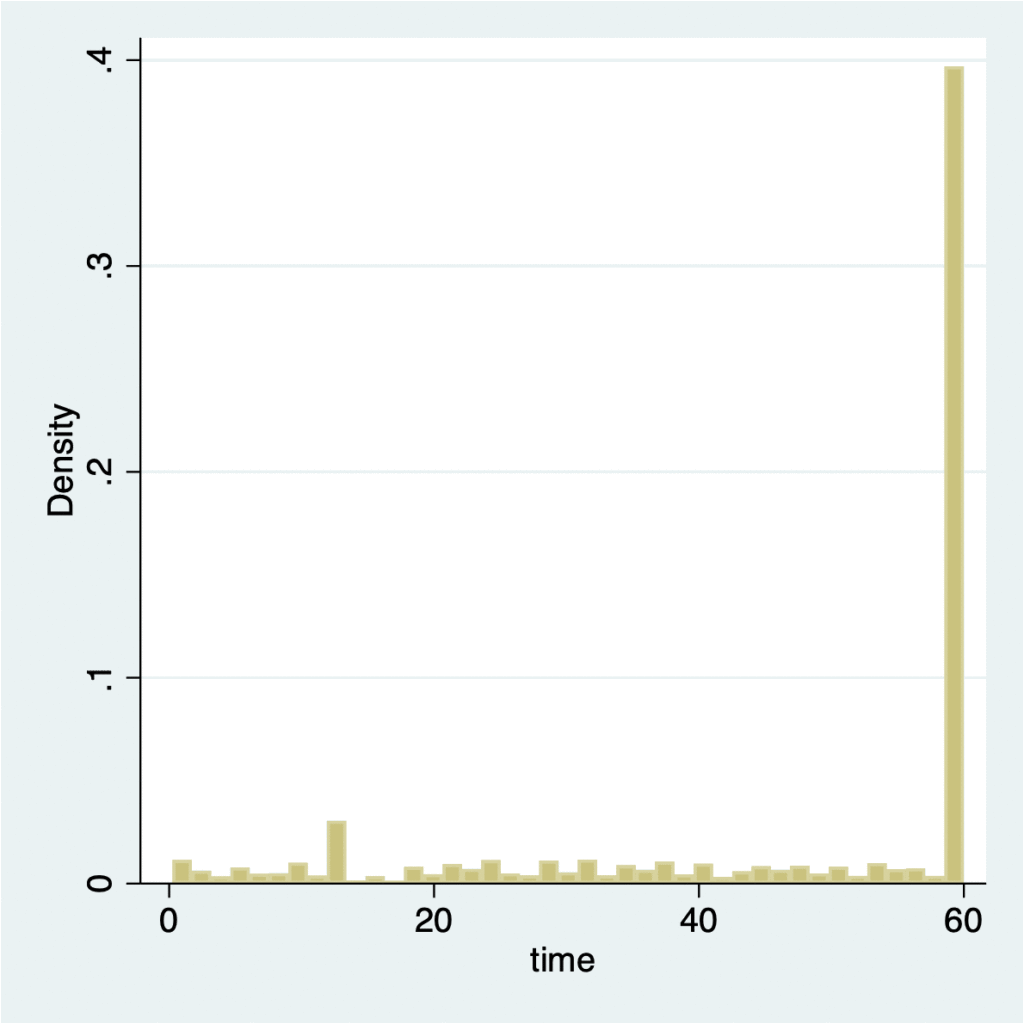
追跡期間time(月)を、0〜1未満、1〜6未満、6〜12未満、12〜24未満、24〜60のカテゴリに区分したdiscrete変数を作成します。
. egen discrete = cut(time), at(0 1 6 12 24 61) icodes
. table discrete, contents(min time max time)
----------------------------------
discrete | min(time) max(time)
----------+-----------------------
0 | .25 .25
1 | 1 5
2 | 6 11
3 | 12 23
4 | 24 60
----------------------------------discrete 0〜4を1〜5に変換します。
. replace discrete = discrete + 1
(3,120 real changes made)ltableコマンドを使って、discrete別に生存率を算出します。noadjustオプションを利用すると、Kaplan-Meier法による生存率が出力されるので、便利です。
. ltable discrete death, noadjust
Beg. Std.
Interval Total Deaths Lost Survival Error [95% Conf. Int.]
-------------------------------------------------------------------------------
1 2 3120 109 9 0.9651 0.0033 0.9580 0.9710
2 3 3002 92 94 0.9355 0.0044 0.9263 0.9436
3 4 2816 66 126 0.9136 0.0051 0.9031 0.9230
4 5 2624 94 238 0.8808 0.0059 0.8687 0.8919
5 6 2292 42 2250 0.8647 0.0063 0.8518 0.8765
-------------------------------------------------------------------------------expand変数を使って、追跡期間(discrete)の分だけレコードを複製します。
. list momid kidid time discrete death if momid==2, clean
momid kidid time discrete death
5. 2 201 60 5 0
6. 2 202 12 4 1
7. 2 203 60 5 0
8. 2 204 1 2 1
. expand discrete
(10,734 observations created)
. sort momid kidid
. list momid kidid time discrete death if momid==2, clean
momid kidid time discrete death
21. 2 201 60 5 0
22. 2 201 60 5 0
23. 2 201 60 5 0
24. 2 201 60 5 0
25. 2 201 60 5 0
26. 2 202 12 4 1
27. 2 202 12 4 1
28. 2 202 12 4 1
29. 2 202 12 4 1
30. 2 203 60 5 0
31. 2 203 60 5 0
32. 2 203 60 5 0
33. 2 203 60 5 0
34. 2 203 60 5 0
35. 2 204 1 2 1
36. 2 204 1 2 1 同一kididのレコードに、連番の変数(interval)を追加します。
. bysort kidid: generate interval = _n
. list momid kidid time discrete interval death if momid==2, clean
momid kidid time discrete interval death
21. 2 201 60 5 1 0
22. 2 201 60 5 2 0
23. 2 201 60 5 3 0
24. 2 201 60 5 4 0
25. 2 201 60 5 5 0
26. 2 202 12 4 1 1
27. 2 202 12 4 2 1
28. 2 202 12 4 3 1
29. 2 202 12 4 4 1
30. 2 203 60 5 1 0
31. 2 203 60 5 2 0
32. 2 203 60 5 3 0
33. 2 203 60 5 4 0
34. 2 203 60 5 5 0
35. 2 204 1 2 1 1
36. 2 204 1 2 2 1 従属変数y=0を作成します。最終追跡時(discrete == interval)ではy=deathに設定します。
. generate y = 0
. replace y = death if interval == discrete
(403 real changes made)
. list momid kidid discrete interval death y if momid==2, clean
momid kidid discrete interval death y
21. 2 201 5 1 0 0
22. 2 201 5 2 0 0
23. 2 201 5 3 0 0
24. 2 201 5 4 0 0
25. 2 201 5 5 0 0
26. 2 202 4 1 1 0
27. 2 202 4 2 1 0
28. 2 202 4 3 1 0
29. 2 202 4 4 1 1
30. 2 203 5 1 0 0
31. 2 203 5 2 0 0
32. 2 203 5 3 0 0
33. 2 203 5 4 0 0
34. 2 203 5 5 0 0
35. 2 204 2 1 1 0
36. 2 204 2 2 1 1 これでdiscrete time hazard model用のデータセットがほぼ完成です。とりあえず、各intervalにおける死亡率を算出してみます。
. tabulate interval y, row
+----------------+
| Key |
|----------------|
| frequency |
| row percentage |
+----------------+
| y
interval | 0 1 | Total
-----------+----------------------+----------
1 | 3,011 109 | 3,120
| 96.51 3.49 | 100.00
-----------+----------------------+----------
2 | 2,910 92 | 3,002
| 96.94 3.06 | 100.00
-----------+----------------------+----------
3 | 2,750 66 | 2,816
| 97.66 2.34 | 100.00
-----------+----------------------+----------
4 | 2,530 94 | 2,624
| 96.42 3.58 | 100.00
-----------+----------------------+----------
5 | 2,250 42 | 2,292
| 98.17 1.83 | 100.00
-----------+----------------------+----------
Total | 13,451 403 | 13,854
| 97.09 2.91 | 100.00 Complementary log-log modelを作成するためには、intervalのダミー変数を作成する必要があります。tabulate, generate()で作成します。
. tabulate interval, generate(int)
interval | Freq. Percent Cum.
------------+-----------------------------------
1 | 3,120 22.52 22.52
2 | 3,002 21.67 44.19
3 | 2,816 20.33 64.52
4 | 2,624 18.94 83.46
5 | 2,292 16.54 100.00
------------+-----------------------------------
Total | 13,854 100.00
. list momid kidid interval int1-int5 death y if momid==2, clean
momid kidid interval int1 int2 int3 int4 int5 death y
21. 2 201 1 1 0 0 0 0 0 0
22. 2 201 2 0 1 0 0 0 0 0
23. 2 201 3 0 0 1 0 0 0 0
24. 2 201 4 0 0 0 1 0 0 0
25. 2 201 5 0 0 0 0 1 0 0
26. 2 202 1 1 0 0 0 0 1 0
27. 2 202 2 0 1 0 0 0 1 0
28. 2 202 3 0 0 1 0 0 1 0
29. 2 202 4 0 0 0 1 0 1 1
30. 2 203 1 1 0 0 0 0 0 0
31. 2 203 2 0 1 0 0 0 0 0
32. 2 203 3 0 0 1 0 0 0 0
33. 2 203 4 0 0 0 1 0 0 0
34. 2 203 5 0 0 0 0 1 0 0
35. 2 204 1 1 0 0 0 0 1 0
36. 2 204 2 0 1 0 0 0 1 1 Discrete time hazard model with complementary log-log model
cloglogコマンドを利用して、complementary log-logモデルを作成します。まずは暴露因子を含まないモデルを作成します。オプションに切片0およびハザード比表示を指定します。
. cloglog y int1-int5, noconstant eform
Iteration 0: log likelihood = -1811.7312
Iteration 1: log likelihood = -1811.6791
Iteration 2: log likelihood = -1811.6791
Complementary log-log regression Number of obs = 13,854
Zero outcomes = 13,451
Nonzero outcomes = 403
Wald chi2(5) = 4943.80
Log likelihood = -1811.6791 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | exp(b) Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
int1 | .0355608 .0034063 -34.83 0.000 .0294738 .0429048
int2 | .0311257 .0032452 -33.28 0.000 .025373 .0381826
int3 | .0237165 .0029194 -30.40 0.000 .0186326 .0301876
int4 | .0364806 .0037629 -32.10 0.000 .0298031 .0446541
int5 | .0184946 .0028538 -25.86 0.000 .0136678 .0250259
------------------------------------------------------------------------------
次に、年齢・性別補正モデルを作成します。
. cloglog y int1-int5 sex mage, noconstant eform
Iteration 0: log likelihood = -1811.344
Iteration 1: log likelihood = -1811.2917
Iteration 2: log likelihood = -1811.2917
Complementary log-log regression Number of obs = 13,854
Zero outcomes = 13,451
Nonzero outcomes = 403
Wald chi2(7) = 4941.87
Log likelihood = -1811.2917 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | exp(b) Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
int1 | .0297238 .0067244 -15.54 0.000 .0190781 .0463097
int2 | .0260221 .0059782 -15.88 0.000 .0165879 .0408218
int3 | .0198284 .004736 -16.41 0.000 .0124158 .0316663
int4 | .0304998 .0069904 -15.23 0.000 .0194629 .0477956
int5 | .0154664 .0039604 -16.28 0.000 .0093633 .0255477
sex | 1.026905 .1024613 0.27 0.790 .8445013 1.248707
mage | 1.00634 .0076432 0.83 0.405 .9914704 1.021432
------------------------------------------------------------------------------母親によるクラスターであると考えれば、Stataではvec(cluster cluster_var)オプションを利用して、robust standard error for clustered dataを求めることができます。
. cloglog y int1-int5 sex mage, noconstant eform vce(cluster momid)
Iteration 0: log pseudolikelihood = -1811.344
Iteration 1: log pseudolikelihood = -1811.2917
Iteration 2: log pseudolikelihood = -1811.2917
Complementary log-log regression Number of obs = 13,854
Zero outcomes = 13,451
Nonzero outcomes = 403
Wald chi2(7) = 4328.62
Log pseudolikelihood = -1811.2917 Prob > chi2 = 0.0000
(Std. Err. adjusted for 851 clusters in momid)
------------------------------------------------------------------------------
| Robust
y | exp(b) Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
int1 | .0297238 .007154 -14.61 0.000 .0185453 .0476403
int2 | .0260221 .0069143 -13.73 0.000 .0154586 .043804
int3 | .0198284 .0053308 -14.58 0.000 .011707 .0335837
int4 | .0304998 .0077332 -13.76 0.000 .0185557 .0501323
int5 | .0154664 .0043305 -14.89 0.000 .0089343 .0267745
sex | 1.026905 .1055175 0.26 0.796 .8395895 1.256012
mage | 1.00634 .0087612 0.73 0.468 .9893139 1.023659
------------------------------------------------------------------------------母親をランダム変数として組み込んだ、random-interceptモデルを作成します。xtcloglogコマンドを利用します。
. xtcloglog y int1-int5 sex mage, noconstant eform i(momid)
Fitting comparison model:
Iteration 0: log likelihood = -1811.344
Iteration 1: log likelihood = -1811.2917
Iteration 2: log likelihood = -1811.2917
Fitting full model:
tau = 0.0 log likelihood = -1911.7661
tau = 0.1 log likelihood = -1893.1909
tau = 0.2 log likelihood = -1874.1809
tau = 0.3 log likelihood = -1856.4094
tau = 0.4 log likelihood = -1842.2824
tau = 0.5 log likelihood = -1834.7269
tau = 0.6 log likelihood = -1837.5067
Iteration 0: log likelihood = -1841.9925
Iteration 1: log likelihood = -1808.6147
Iteration 2: log likelihood = -1806.9026
Iteration 3: log likelihood = -1806.7965
Iteration 4: log likelihood = -1806.7963
Iteration 5: log likelihood = -1806.7963
Random-effects complementary log-log model Number of obs = 13,854
Group variable: momid Number of groups = 851
Random effects u_i ~ Gaussian Obs per group:
min = 1
avg = 16.3
max = 40
Integration method: mvaghermite Integration pts. = 12
Wald chi2(7) = 2450.04
Log likelihood = -1806.7963 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
y | exp(b) Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
int1 | .0277072 .0065873 -15.08 0.000 .0173869 .0441532
int2 | .0245443 .0059068 -15.40 0.000 .0153144 .0393369
int3 | .0188305 .004693 -15.94 0.000 .0115538 .0306903
int4 | .0291856 .0069987 -14.74 0.000 .0182411 .0466969
int5 | .0149082 .0039561 -15.85 0.000 .0088623 .0250786
sex | 1.033765 .1049692 0.33 0.744 .8472088 1.261402
mage | 1.003026 .0081413 0.37 0.710 .9871959 1.019111
-------------+----------------------------------------------------------------
/lnsig2u | -1.254711 .3784523 -1.996464 -.5129578
-------------+----------------------------------------------------------------
sigma_u | .5340022 .1010472 .3685305 .7737713
rho | .1477433 .0476529 .0762683 .2668511
------------------------------------------------------------------------------
Note: Estimates are transformed only in the first equation.
LR test of rho=0: chibar2(01) = 8.99 Prob >= chibar2 = 0.001